Difference between revisions of "Table of contents"
From Polyfolds.org
Natebottman (Talk | contribs) |
Natebottman (Talk | contribs) |
||
| Line 21: | Line 21: | ||
* [[Deligne-Mumford space]] (Nate-work-in-progress) | * [[Deligne-Mumford space]] (Nate-work-in-progress) | ||
| − | ** [[Deligne-Mumford space#Gluing and the definition of the topology]] (N-TODO .. or replace reference to this in [[http://www.polyfolds.org/index.php?title=Moduli_spaces_of_pseudoholomorphic_polygons#General_moduli_space_of_pseudoholomorphic_polygons expansion of expansion in point 7]] and [[Gluing construction for Hamiltonians]] ) | + | ** [[Deligne-Mumford space#Gluing and the definition of the topology|glued surface]] (N-TODO .. or replace reference to this in [[http://www.polyfolds.org/index.php?title=Moduli_spaces_of_pseudoholomorphic_polygons#General_moduli_space_of_pseudoholomorphic_polygons expansion of expansion in point 7]] and [[Gluing construction for Hamiltonians]] ) |
* [[Compactified Morse trajectory spaces]] (brief summary with references - could use extension) | * [[Compactified Morse trajectory spaces]] (brief summary with references - could use extension) | ||
* [[Coherent orientations on the regularized moduli spaces]] arising from polyfold theory (TODO) | * [[Coherent orientations on the regularized moduli spaces]] arising from polyfold theory (TODO) | ||
Revision as of 13:01, 9 June 2017
Table of contents for Polyfold Constructions for Fukaya Categories
Construction overviews:
- Moduli spaces of pseudoholomorphic polygons
- Regularized moduli spaces
- summary of resulting Floer chain complex (TODO)
Algebra details:
- Novikov ring (TODO)
- Brane structure (TODO)
- Orientations of Cauchy-Riemann sections induced by brane structures (TODO)
Geometry/Topology/Combinatorics details:
- Deligne-Mumford space (Nate-work-in-progress)
- glued surface (N-TODO .. or replace reference to this in [expansion of expansion in point 7] and Gluing construction for Hamiltonians )
- Compactified Morse trajectory spaces (brief summary with references - could use extension)
- Coherent orientations on the regularized moduli spaces arising from polyfold theory (TODO)
- the polyfold ambient space
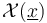 as a topological space (K-TODO)
as a topological space (K-TODO)
- Gromov topology (K-TODO)
- the polyfold ambient bundle
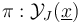 as continuous surjection between topological spaces (K-TODO)
as continuous surjection between topological spaces (K-TODO) - the Cauchy-Riemann section as continuous map
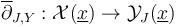 (K-TODO)
(K-TODO)
Analysis details:
- the polyfold smooth structure on the ambient space
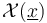 (J-TODO)
(J-TODO) - the polyfold bundle structure of the ambient bundle
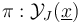 (J-TODO)
(J-TODO) - the polyfold Fredholm property of the Cauchy-Riemann section
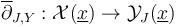 (J-TODO)
(J-TODO) - proof that Gromov compactness implies properness of the Cauchy-Riemann section (TODO)