Regularized moduli spaces
Contents
Abstract, Coherent Regularization
In order to regularize the moduli spaces of pseudoholomorphic polygons 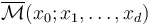 for each tuple of Lagrangians
for each tuple of Lagrangians 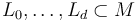 , generators
, generators 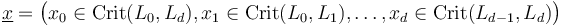 , and a fixed compatible almost complex structure
, and a fixed compatible almost complex structure 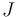 , any abstract regularization approach (opposed to geometric ones, as contrasted in [section 3, FFGW] and [sections 2.1-2, MW]) starts by describing each Gromov-compactified moduli space as
, any abstract regularization approach (opposed to geometric ones, as contrasted in [section 3, FFGW] and [sections 2.1-2, MW]) starts by describing each Gromov-compactified moduli space as
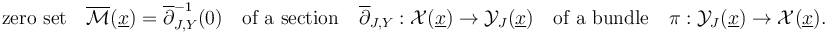
In order to obtain boundary stratifications which imply the 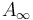 -relations, any abstract approach needs to regularize "coherently" (whereas geometric regularizations are automatically coherent), that is compatible with the boundary stratification of the ambient spaces
-relations, any abstract approach needs to regularize "coherently" (whereas geometric regularizations are automatically coherent), that is compatible with the boundary stratification of the ambient spaces 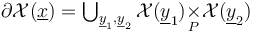 being given by fiber products (over some evaluation maps to a space
being given by fiber products (over some evaluation maps to a space  ) of other ambient spaces. A little more precisely, in this general fiber product description, the regularizations
) of other ambient spaces. A little more precisely, in this general fiber product description, the regularizations 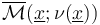 need to have a notion of boundary for which Stokes' theorem holds and
need to have a notion of boundary for which Stokes' theorem holds and 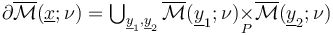 .
.
In our setup, these fiber products are over finite sets of Morse and Floer critical points, so simplify to unions of Cartesian products,
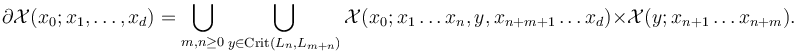
These Cartesian products have overlaps in the corners of 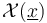 .
We can further specify this stratification by considering the boundary strata
.
We can further specify this stratification by considering the boundary strata
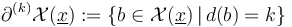 with specific (boundary) degeneracy index (see [Section 3.1 HWZ-III] and [Section 5.3, FFGW]) - in particular denoting the interior of the ambient polyfolds by
with specific (boundary) degeneracy index (see [Section 3.1 HWZ-III] and [Section 5.3, FFGW]) - in particular denoting the interior of the ambient polyfolds by 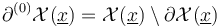 and the smooth part of the boundary (excluding corners) by
and the smooth part of the boundary (excluding corners) by
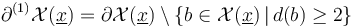 . With this notation, we can express the fact that the smooth part of the boundary is the disjoint union of Cartesian products of interiors,
. With this notation, we can express the fact that the smooth part of the boundary is the disjoint union of Cartesian products of interiors,
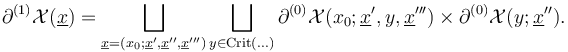
If we now think of the regularizations as zero sets of a transversely perturbed section, 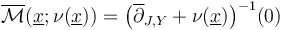 , then the coherence requirement can be guaranteed if the restriction of any perturbation
, then the coherence requirement can be guaranteed if the restriction of any perturbation 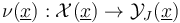 to each boundary component
is given by the product of perturbations associated to the splitting of the boundary component,
to each boundary component
is given by the product of perturbations associated to the splitting of the boundary component,
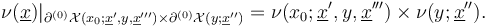
In the abstract regularization approach of [2015-FOOO1], [2017-FOOO2], and most other virtual approaches, the global sections  are patched together from smooth sections of finite rank bundles over finite dimensional manifolds
are patched together from smooth sections of finite rank bundles over finite dimensional manifolds 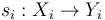 .
These local sections are obtained by 'finite dimensional reduction' of local Fredholm descriptions of the moduli spaces, but are no longer directly identified with Cauchy-Riemann operators. Another undesirable feature of this approach is that the local Kuranishi ambient spaces
.
These local sections are obtained by 'finite dimensional reduction' of local Fredholm descriptions of the moduli spaces, but are no longer directly identified with Cauchy-Riemann operators. Another undesirable feature of this approach is that the local Kuranishi ambient spaces 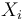 are generally 'too small' to allow for straight-forward constructions of new moduli spaces (e.g. by restriction to curves having certain intersection properties, or coupling of curves with each other or Morse trajectories) via restrictions or fiber products of the local sections.
are generally 'too small' to allow for straight-forward constructions of new moduli spaces (e.g. by restriction to curves having certain intersection properties, or coupling of curves with each other or Morse trajectories) via restrictions or fiber products of the local sections.
While at first glance the finite dimensional reductions in virtual approaches resolve most analytic issues (up to the question of obtaining smooth sections near nodal curves from the classical gluing analysis), it introduces a number of subtle combinatorial, algebraic, and topological challenges as discussed in [MW].
Many of these challenges stem from the lack of a natural ambient space, which is replaced by a highly choice-dependent space 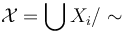 that is constructed from nontrivial notions of transition data between the local base manifolds
that is constructed from nontrivial notions of transition data between the local base manifolds 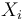 of different dimensions.
To see why the Kuranishi charts
of different dimensions.
To see why the Kuranishi charts 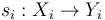 are generally 'too small' to allow for restrictions or fiber products of the local sections, note that such constructions require transversality of evaluation maps whose domains are the local ambient spaces
are generally 'too small' to allow for restrictions or fiber products of the local sections, note that such constructions require transversality of evaluation maps whose domains are the local ambient spaces 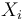 . So these would need to be constructed with the particular transversality in mind - which may not be possible if e.g. transversality to an uncountable set of chains is desired.
. So these would need to be constructed with the particular transversality in mind - which may not be possible if e.g. transversality to an uncountable set of chains is desired.
In the abstract regularization approach via polyfold theory [HWZ], the ambient space 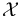 is infinite dimensional and chosen ‘large enough’ to be fairly natural, allow for restrictions and fiber products, and so that the section
is infinite dimensional and chosen ‘large enough’ to be fairly natural, allow for restrictions and fiber products, and so that the section 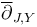 is directly given by a Cauchy-Riemann operator.
While this resolves most combinatorial, algebraic, and topological challenges - by building a natural ambient space that is e.g. Hausdorff and provides natural compactness controls - equipping this ambient space with a notion of smooth structure posed analytic issues that were insurmountable with classical infinite dimensional analysis.
is directly given by a Cauchy-Riemann operator.
While this resolves most combinatorial, algebraic, and topological challenges - by building a natural ambient space that is e.g. Hausdorff and provides natural compactness controls - equipping this ambient space with a notion of smooth structure posed analytic issues that were insurmountable with classical infinite dimensional analysis.
Polyfold Fredholm Descriptions of Moduli spaces
To overcome the analytic challenges, the abstract parts of polyfold theory provide alternative notions of infinite dimensional spaces and differentiability with which we will be able to
- equip each ambient space
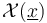 with a smooth structure as 'polyfold modeled on sc-Hilbert spaces';
with a smooth structure as 'polyfold modeled on sc-Hilbert spaces';
- equip each ambient bundle
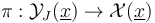 with a smooth bundle structure as 'strong polyfold bundle over
with a smooth bundle structure as 'strong polyfold bundle over 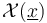 ';
';
- show that each Cauchy-Riemann section
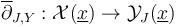 satisfies adapted notions of smoothness and nonlinear Fredholm properties, i.e. is a 'sc-Fredholm section of the polyfold bundle
satisfies adapted notions of smoothness and nonlinear Fredholm properties, i.e. is a 'sc-Fredholm section of the polyfold bundle 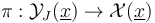 '.
'.
Before we can use the abstract perturbation results from polyfold theory to regularize the zero sets 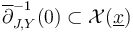 , we need to restrict ourselves to (unions of) connected components of the ambient space within which the zero set is compact.
Moreover, we will ultimately just need the zero sets of specific Fredholm indices. So for any
, we need to restrict ourselves to (unions of) connected components of the ambient space within which the zero set is compact.
Moreover, we will ultimately just need the zero sets of specific Fredholm indices. So for any 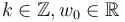 we define
we define
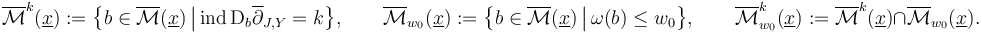
Here the linearized section 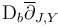 has a well defined Fredholm index in
has a well defined Fredholm index in 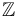 at any solution
at any solution 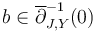 , and
, and 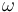 is the symplectic area function defined on moduli spaces of pseudoholomorphic polygons. We will extend both to locally constant functions on the ambient spaces,
is the symplectic area function defined on moduli spaces of pseudoholomorphic polygons. We will extend both to locally constant functions on the ambient spaces,
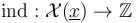 and
and 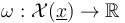 , and thus obtain ambient spaces for
, and thus obtain ambient spaces for
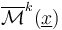 and
and 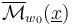 ,
,

Now Gromov compactness can be formulated as saying that for any 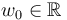 the restricted section
the restricted section 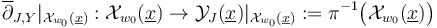 is a proper Fredholm section (of a strong polyfold bundle over a polyfold that is modeled on sc-Hilbert spaces).
is a proper Fredholm section (of a strong polyfold bundle over a polyfold that is modeled on sc-Hilbert spaces).
Indeed, [Definition 4.1 HWZ-III] of a section being proper requires the zero set 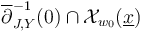 to be compact, and we will show that Gromov compactness implies properness.
to be compact, and we will show that Gromov compactness implies properness.
Polyfold Regularizations
In the special case of trivial isotropy - when each 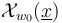 is an M-polyfold - the abstract M-polyfold perturbation and implicit function theorem package [Theorem 5.18 HWZ-1] then provides, for any
is an M-polyfold - the abstract M-polyfold perturbation and implicit function theorem package [Theorem 5.18 HWZ-1] then provides, for any 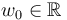 , a perturbation
, a perturbation 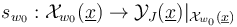 that is transverse to
that is transverse to 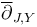 , in general position to the boundary&corners of
, in general position to the boundary&corners of 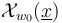 , and controls compactness such that the perturbed solution set
, and controls compactness such that the perturbed solution set
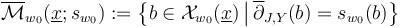
inherits the structure of a compact manifold whose dimension near 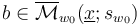 is given by the Fredholm index
is given by the Fredholm index 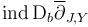 .
.
Moreover, the boundary and corner strata of the perturbed solution set are given by transverse general position intersections with the boundary and corner strata of the ambient M-polyfold 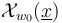 in the sense that
in the sense that
for each corner degeneracy index 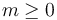 (with
(with 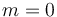 denoting the interior and
denoting the interior and 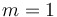 the main stratum of the boundary) we have
the main stratum of the boundary) we have 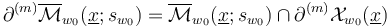 cut out transversely by the restriction
cut out transversely by the restriction 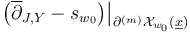 , which has Fredholm index
, which has Fredholm index 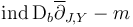 .
In particular:
.
In particular:
- The index
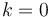 part of the perturbed moduli space
part of the perturbed moduli space 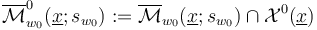 is a compact 0-manifold that does not intersect the boundary of the ambient M-polyfold.
is a compact 0-manifold that does not intersect the boundary of the ambient M-polyfold. - The
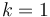 -dimensional part of the perturbed moduli space
-dimensional part of the perturbed moduli space 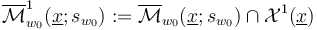 is a compact 1-manifold with boundary
is a compact 1-manifold with boundary 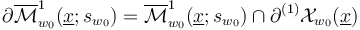 .
.
This will be used - in the setting of possibly nontrivial isotropy - in the proof of the 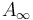 -relations.
-relations.
We will see below that this perturbation section 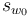 can in fact be extended to all of
can in fact be extended to all of 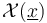 . However, in the case of nontrivial isotropy, we will have to work with multisections
. However, in the case of nontrivial isotropy, we will have to work with multisections 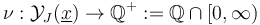 . These are related to sections in the case of trivial isotropy by a section
. These are related to sections in the case of trivial isotropy by a section 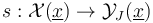 inducing a multisection given by
inducing a multisection given by 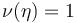 iff
iff 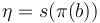 , and
, and 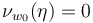 otherwise.
In the general case of nontrivial isotropy, we moreover require orientations of Cauchy-Riemann sections before we can construct a multisection
otherwise.
In the general case of nontrivial isotropy, we moreover require orientations of Cauchy-Riemann sections before we can construct a multisection 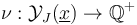 such that the perturbed solution set
such that the perturbed solution set
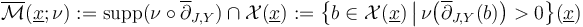
inherits the structure of a branched suborbifold of the polyfold 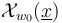 such that
such that 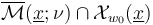 is compact for any
is compact for any 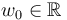 .
.
This branched orbifold will also inherit a weight function, which (by abuse of notation) we denote 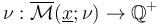 .
.
At points with nontrivial isotropy, the weight is in fact given by the restriction of 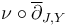 , multiplied by a sign arising from the coherent orientations on the regularized moduli spaces.
At points with nontrivial isotopy, this signed value of
, multiplied by a sign arising from the coherent orientations on the regularized moduli spaces.
At points with nontrivial isotopy, this signed value of 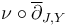 needs to be divided by the order of the isotropy group.
needs to be divided by the order of the isotropy group.
The construction of 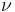 is based on [Theorem 4.19 HWZ-III],
is based on [Theorem 4.19 HWZ-III],
which we apply to obtain - for any fixed 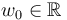 - a multisection
- a multisection 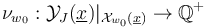 that is transverse to
that is transverse to 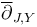 and controls compactness such that the solution set
and controls compactness such that the solution set
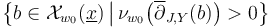 is a compact branched suborbifold of the polyfold
is a compact branched suborbifold of the polyfold 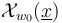 with boundary and corners.
We can moreover perform this construction for a sequence
with boundary and corners.
We can moreover perform this construction for a sequence 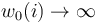 and in each step choose the multisection
and in each step choose the multisection 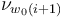 to coincide on
to coincide on 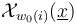 with the (already transverse on these components) perturbation
with the (already transverse on these components) perturbation 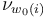 .
Then the required perturbation
.
Then the required perturbation 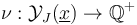 can be obtained as the limit
can be obtained as the limit
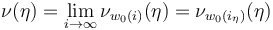 , where
, where 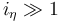 such that
such that 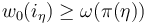 .
.
Moreover, by choosing 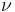 in 'general position', we can ensure that the boundary and corner strata of the perturbed solution set are given by transverse intersections with the boundary and corner strata of the ambient polyfold
in 'general position', we can ensure that the boundary and corner strata of the perturbed solution set are given by transverse intersections with the boundary and corner strata of the ambient polyfold 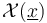 . In particular, the proof of the
. In particular, the proof of the 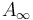 -relations in the polyfold constructions for Fukaya categories is based on the following two special cases:
-relations in the polyfold constructions for Fukaya categories is based on the following two special cases:
- The index
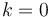 part of the perturbed moduli space
part of the perturbed moduli space 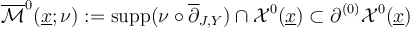 is a 0-dimensional manifold contained in the interior of the ambient polyfold with weight function
is a 0-dimensional manifold contained in the interior of the ambient polyfold with weight function 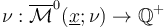 .
. - The
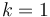 -dimensional part of the perturbed moduli space
-dimensional part of the perturbed moduli space 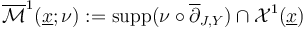 is a 1-dimensional branched suborbifold of the ambient polyfold with weight function
is a 1-dimensional branched suborbifold of the ambient polyfold with weight function 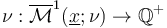 and boundary
and boundary 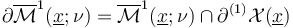 .
.
Since the boundary&corner stratification of the ambient polyfold 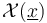 is given,
the coherence required for the
is given,
the coherence required for the 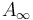 -relations can then be achieved by constructing the perturbation
-relations can then be achieved by constructing the perturbation 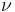 coherently, i.e. such that for every decomposition
coherently, i.e. such that for every decomposition
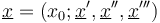 into
into
 and corresponding generator
and corresponding generator
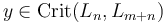 ,
the perturbation
,
the perturbation 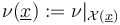 is given on each smooth boundary stratum by products of the perturbations on the ambient polyfolds indicated by the splitting of the generators,
is given on each smooth boundary stratum by products of the perturbations on the ambient polyfolds indicated by the splitting of the generators,
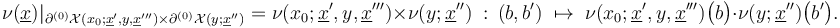
To see why this implies the required coherence of regularizations
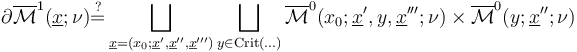 ,
note that the above identities for the boundary strata of the perturbed solution spaces and ambient polyfolds allow us to express the coherence requirements as
,
note that the above identities for the boundary strata of the perturbed solution spaces and ambient polyfolds allow us to express the coherence requirements as
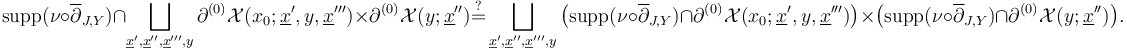
In the case of trivial isotropy, an inductive construction of such coherent perturbations is given in a preprint draft by Ben Filippenko. Unfortunately, the generalization of this construction to nontrivial isotropy requires the resolution of a surprisingly nontrivial issue of extending multisections given on boundaries and corners to the interior of a polyfold. In fact, this same issue already appears in finite dimensions for multisections of orbi-bundles with boundary and corners. It is being resolved in a not yet available manuscript by Hofer-Wysocki-Zehnder.
Construction of Composition Operations
For the Composition Operators in the polyfold constructions for Fukaya categories to be well defined we need to check that 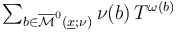 defines an element in the Novikov ring. This requires the following two properties of the perturbed solution sets:
defines an element in the Novikov ring. This requires the following two properties of the perturbed solution sets:
Every perturbed solution 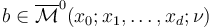 needs to have nonnegative symplectic area
needs to have nonnegative symplectic area 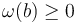 . This is achieved as follows:
. This is achieved as follows:
If all Lagrangians involved are pairwise either identical or transverse, then no Hamiltonian perturbations to the Cauchy-Riemann equation are involved in the construction of the unperturbed moduli space 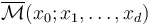 . Thus each component
. Thus each component 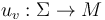 of an unperturbed solution satisfies
of an unperturbed solution satisfies
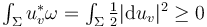 , and this sums up to
, and this sums up to 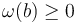 .
Thus the Cauchy-Riemann operator
.
Thus the Cauchy-Riemann operator 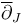 has no zeros in the connected components
has no zeros in the connected components 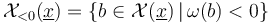 of negative symplectic area. Since transversality is a condition only at solutions, this means we can fix the perturbation
of negative symplectic area. Since transversality is a condition only at solutions, this means we can fix the perturbation 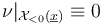 on the connected components of the ambient space of negative energy. As a result, all perturbed solutions will satisfy
on the connected components of the ambient space of negative energy. As a result, all perturbed solutions will satisfy 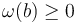 , as required.
, as required.
Here input from the Mirror Symmetry community is needed
on how to define 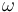 , or which kind of Novikov coefficients to use, in the presence of Hamiltonian perturbations for nontransverse pairs of nonidentical Lagrangians.
, or which kind of Novikov coefficients to use, in the presence of Hamiltonian perturbations for nontransverse pairs of nonidentical Lagrangians.
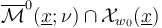 of Fredholm index
of Fredholm index 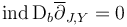 and bounded energy
and bounded energy 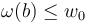 for some
for some 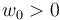 needs to be a finite set.
needs to be a finite set.
This is true by the following:
First, preservation of compactness in the polyfold regularization (as discussed above) guarantees that 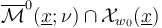 is a compact set.
Second, the implicit function theorem for transverse sc-Fredholm multisections of polyfold bundles implies that the set of perturbed solutions of Fredholm index 0,
is a compact set.
Second, the implicit function theorem for transverse sc-Fredholm multisections of polyfold bundles implies that the set of perturbed solutions of Fredholm index 0, 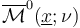 carries the structure of a 0-dimensional weighted-branched orbifold.
Together, this implies that
carries the structure of a 0-dimensional weighted-branched orbifold.
Together, this implies that 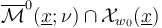 is a finite set, as claimed. (The weighted-branching structure is expressed in the weight function
is a finite set, as claimed. (The weighted-branching structure is expressed in the weight function 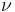 .)
</math>
.)
</math>
Proof of 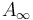 -relations
-relations
As explained in polyfold constructions for Fukaya categories, this proof follows from coherence of the regularizations,
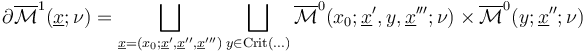
together with the following two relations at boundary points 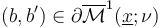 corresponding to pairs of
corresponding to pairs of 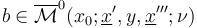 and
and 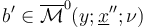 :
:
1. Multiplicativity of weight functions 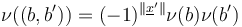 is achieved by
is achieved by
- coherent construction of the multisections,
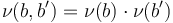 ;
; - the observation that the isotropy groups in Cartesian products are multiplicative;
- coherent orientations on the regularized moduli spaces which in particular yield the sign
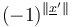 .
.
 holds by construction of the symplectic area function.
holds by construction of the symplectic area function.