Gluing construction for Hamiltonians
From Polyfolds.org
TODO: As cited in [expansion of expansion in point 7], construct vector-field-valued 1-forms 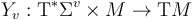 on
on 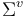 compatibly with the fixed Hamiltonian perturbations.
compatibly with the fixed Hamiltonian perturbations.
Copies from moduli spaces of pseudoholomorphic polygons:
- On the thin part
![\iota _{e}^{v}:[0,\infty )\times [0,1]\hookrightarrow \Sigma ^{v}](/images/math/d/1/1/d1100c1e7510c1014aac509f6b8fd6de.png) near each puncture
near each puncture 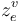 we have
we have 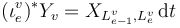 .
.
- Note that this convention together with our symmetric choice of Hamiltonian perturbations
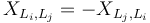 forces the vector-field-valued 1-form on
forces the vector-field-valued 1-form on ![\Sigma ^{v}\simeq \mathbb{R} \times [0,1]](/images/math/5/6/a/56a3486ce4c38533929719c2fae3d318.png) in case
in case 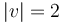 to be
to be 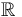 -invariant,
-invariant, 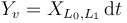 if
if 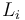 are the Lagrangian labels for the boundary components
are the Lagrangian labels for the boundary components 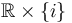 .
.
- Here and in the following we denote
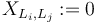 in case
in case  , so that
, so that 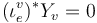 in case
in case 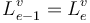 .
.
- The Hamiltonian perturbations
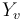 should be cut off to vanish outside of the thin parts of the domains
should be cut off to vanish outside of the thin parts of the domains 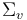 . However, there may be thin parts of a surface
. However, there may be thin parts of a surface 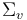 that are not neighborhoods of a puncture. On these, we must choose the Hamiltonian-vector-field-valued one-form
that are not neighborhoods of a puncture. On these, we must choose the Hamiltonian-vector-field-valued one-form 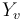 compatible with gluing as in [Seidel book].
compatible with gluing as in [Seidel book].
- For example, in the neighbourhood of a tree with an edge
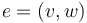 between main vertices, there are trees in which this edge is removed, the two vertices are replaced by a single vertex
between main vertices, there are trees in which this edge is removed, the two vertices are replaced by a single vertex 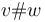 , and the surfaces
, and the surfaces 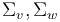 are replaced by a single glued surface (or find reference in Deligne-Mumford space)
are replaced by a single glued surface (or find reference in Deligne-Mumford space) 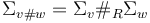 for
for 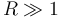 . Compatibility with gluing requires that the Hamiltonian perturbation on these glued surfaces is also given by a gluing construction
. Compatibility with gluing requires that the Hamiltonian perturbation on these glued surfaces is also given by a gluing construction 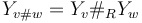 (in which the two perturbations
(in which the two perturbations 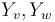 agree and hence can be matched over a long neck
agree and hence can be matched over a long neck ![[-R,R]\times [0,1]\subset \Sigma _{{v\#w}}](/images/math/7/c/1/7c10420071147771af7f4f746f0fc075.png) ).
).