Difference between revisions of "Regularized moduli spaces"
Natebottman (Talk | contribs) (→Abstract, Coherent Regularization) |
Natebottman (Talk | contribs) (→Abstract, Coherent Regularization) |
||
| Line 13: | Line 13: | ||
</math> | </math> | ||
</center> | </center> | ||
| − | In order to obtain boundary stratifications which imply the <math>A_\infty</math>-relations, any abstract approach needs to regularize | + | In order to obtain boundary stratifications which imply the <math>A_\infty</math>-relations, any abstract approach needs to regularize "coherently’’ (whereas geometric regularizations are automatically coherent), that is compatible with the boundary stratification of the ambient spaces <math>\mathcal{X}(\underline{x})</math> being given by fiber products of other ambient spaces. In our setup, these fiber products are over finite sets of Morse and Floer critical points, so simplify to unions of Cartesian products, |
<center> | <center> | ||
<math> | <math> | ||
Revision as of 13:10, 3 June 2017
Contents
Abstract, Coherent Regularization
In order to regularize the moduli spaces of pseudoholomorphic polygons 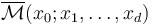 for each tuple of Lagrangians
for each tuple of Lagrangians 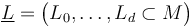 , generators
, generators 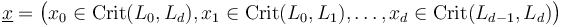 , and a fixed compatible almost complex structure
, and a fixed compatible almost complex structure  , any abstract regularization approach (opposed to geometric ones, as contrasted in [section 3, FFGW] and [sections 2.1-2, MW]) starts by describing each Gromov-compactified moduli space as
, any abstract regularization approach (opposed to geometric ones, as contrasted in [section 3, FFGW] and [sections 2.1-2, MW]) starts by describing each Gromov-compactified moduli space as
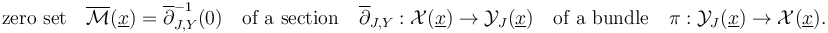
In order to obtain boundary stratifications which imply the 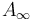 -relations, any abstract approach needs to regularize "coherently’’ (whereas geometric regularizations are automatically coherent), that is compatible with the boundary stratification of the ambient spaces
-relations, any abstract approach needs to regularize "coherently’’ (whereas geometric regularizations are automatically coherent), that is compatible with the boundary stratification of the ambient spaces 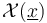 being given by fiber products of other ambient spaces. In our setup, these fiber products are over finite sets of Morse and Floer critical points, so simplify to unions of Cartesian products,
being given by fiber products of other ambient spaces. In our setup, these fiber products are over finite sets of Morse and Floer critical points, so simplify to unions of Cartesian products,
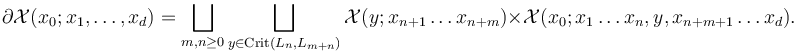
In the abstract regularization approach of [2015-FOOO1], [2017-FOOO2], and most other virtual approaches, the global sections 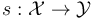 are patched together from smooth sections of finite rank bundles over finite dimensional manifolds
are patched together from smooth sections of finite rank bundles over finite dimensional manifolds 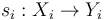 .
While at first glance this resolves most analytic issues (up to the question of obtaining smooth sections near nodal curves from the classical gluing analysis), it introduces a number of subtle combinatorial, algebraic, and topological challenges as discussed in [MW].
.
While at first glance this resolves most analytic issues (up to the question of obtaining smooth sections near nodal curves from the classical gluing analysis), it introduces a number of subtle combinatorial, algebraic, and topological challenges as discussed in [MW].
Many of these challenges stem from the lack of a natural ambient space, which is replaced by a highly choice-dependent space 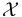 that is constructed from nontrivial notions of transition data between the local base manifolds
that is constructed from nontrivial notions of transition data between the local base manifolds 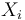 of different dimensions.
Other undesirable features of this approach are that the sections
of different dimensions.
Other undesirable features of this approach are that the sections 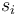 are no longer directly identified with Cauchy-Riemann operators, and that the Kuranishi charts
are no longer directly identified with Cauchy-Riemann operators, and that the Kuranishi charts 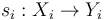 are generally 'too small' to allow for straight-forward constructions of new moduli spaces (e.g. by restriction to curves having certain intersection properties, or coupling of curves with each other or Morse trajectories) via restrictions or fiber products of the local sections. (Such constructions require transversality of evaluation maps
whose domain is the ambient space
are generally 'too small' to allow for straight-forward constructions of new moduli spaces (e.g. by restriction to curves having certain intersection properties, or coupling of curves with each other or Morse trajectories) via restrictions or fiber products of the local sections. (Such constructions require transversality of evaluation maps
whose domain is the ambient space 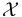 , which would need to be constructed with the particular transversality in mind.)
, which would need to be constructed with the particular transversality in mind.)
In the abstract regularization approach via polyfold theory [HWZ], the ambient space 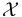 is chosen ‘large enough’ to be fairly natural, allow for restrictions and fiber products, and so that the section
is chosen ‘large enough’ to be fairly natural, allow for restrictions and fiber products, and so that the section 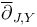 is directly given by a Cauchy-Riemann operator.
While this resolves most combinatorial, algebraic, and topological challenges - by building a natural ambient space that is e.g. Hausdorff and provides natural compactness controls - equipping this ambient space with a notion of smooth structure posed analytic issues that were insurmountable with classical infinite dimensional analysis.
is directly given by a Cauchy-Riemann operator.
While this resolves most combinatorial, algebraic, and topological challenges - by building a natural ambient space that is e.g. Hausdorff and provides natural compactness controls - equipping this ambient space with a notion of smooth structure posed analytic issues that were insurmountable with classical infinite dimensional analysis.
Polyfold Fredholm Descriptions of Moduli spaces
To overcome the analytic challenges, the abstract parts of polyfold theory provide alternative notions of infinite dimensional spaces and differentiability with which we will be able to
- equip each ambient space
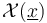 with a smooth structure as 'polyfold modeled on sc-Hilbert spaces';
with a smooth structure as 'polyfold modeled on sc-Hilbert spaces';
- equip each ambient bundle
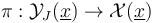 with a smooth bundle structure as 'strong polyfold bundle over
with a smooth bundle structure as 'strong polyfold bundle over 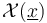 ';
';
- show that each Cauchy-Riemann section
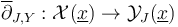 satisfies adapted notions of smoothness and nonlinear Fredholm properties, i.e. is a 'sc-Fredholm section of the polyfold bundle
satisfies adapted notions of smoothness and nonlinear Fredholm properties, i.e. is a 'sc-Fredholm section of the polyfold bundle 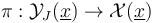 '.
'.
Before we can use the abstract perturbation results from polyfold theory to regularize the zero sets 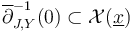 , we need to restrict ourselves to (unions of) connected components of the ambient space within which the zero set is compact.
Moreover, we will ultimately just need the zero sets of specific Fredholm indices. So for any
, we need to restrict ourselves to (unions of) connected components of the ambient space within which the zero set is compact.
Moreover, we will ultimately just need the zero sets of specific Fredholm indices. So for any 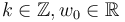 we define
we define
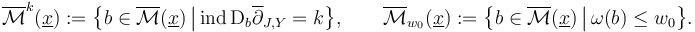
Here the linearized section 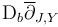 has a well defined Fredholm index in
has a well defined Fredholm index in 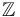 at any solution
at any solution 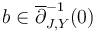 , and
, and 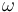 is the symplectic area function defined on Moduli spaces of pseudoholomorphic polygons. We will extend both to locally constant functions on the ambient spaces,
is the symplectic area function defined on Moduli spaces of pseudoholomorphic polygons. We will extend both to locally constant functions on the ambient spaces,
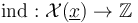 and
and 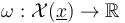 , and thus obtain ambient spaces for
, and thus obtain ambient spaces for
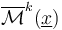 and
and 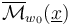 ,
,

Now Gromov compactness can be formulated as saying that for any  the restricted section
the restricted section 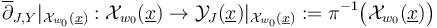 is a proper Fredholm section (of a strong polyfold bundle over a polyfold that is modeled on sc-Hilbert spaces).
is a proper Fredholm section (of a strong polyfold bundle over a polyfold that is modeled on sc-Hilbert spaces).
Indeed, [Definition 4.1 HWZIII] of a section being proper requires the zero set 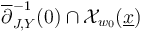 to be compact, and we will show that Gromov compactness implies properness.
to be compact, and we will show that Gromov compactness implies properness.
Polyfold Regularizations
In the special case of trivial isotropy - when each 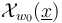 is an M-polyfold - the abstract M-polyfold perturbation and implicit function theorem package [Theorem 5.18 HWZ] then provides, for any
is an M-polyfold - the abstract M-polyfold perturbation and implicit function theorem package [Theorem 5.18 HWZ] then provides, for any 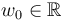 , a perturbation
, a perturbation 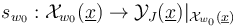 that is transverse to
that is transverse to 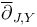 and controls compactness such that the perturbed solution set
and controls compactness such that the perturbed solution set
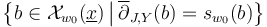 inherits the structure of a compact manifold with boundary and corners induced by intersections with the boundary and corner structures of
inherits the structure of a compact manifold with boundary and corners induced by intersections with the boundary and corner structures of 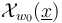 .
We will see below that this perturbation section
.
We will see below that this perturbation section 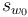 can in fact be extended to all of
can in fact be extended to all of 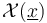 . However, in the case of nontrivial isotropy, we will have to work with multi-sections
. However, in the case of nontrivial isotropy, we will have to work with multi-sections 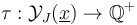 . These are related to sections in the case of trivial isotropy by a section
. These are related to sections in the case of trivial isotropy by a section 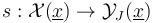 inducing a multi-section given by
inducing a multi-section given by 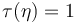 iff
iff 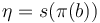 , and
, and 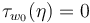 otherwise.
otherwise.
In the general case of nontrivial isotropy, we moreover require orientations of Cauchy-Riemann sections before we can construct a multi-valued perturbation 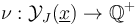 such that the perturbed solution set
such that the perturbed solution set
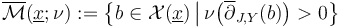
is a branched suborbifold of the polyfold 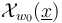 such that
such that 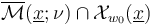 is compact for any
is compact for any 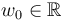 .
(Moreover, this branched orbifold is weighted by the restriction
.
(Moreover, this branched orbifold is weighted by the restriction 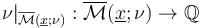 .)
.)
To construct 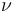 we first apply [Theorem 4.19 HWZIII] to obtain - for any fixed
we first apply [Theorem 4.19 HWZIII] to obtain - for any fixed 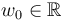 - a multi-valued perturbation
- a multi-valued perturbation 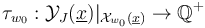 that is transverse to
that is transverse to 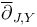 and controls compactness such that the solution set
and controls compactness such that the solution set
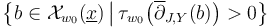 is a compact branched suborbifold of the polyfold
is a compact branched suborbifold of the polyfold 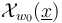 with boundary and corners.
We can moreover perform this construction for a sequence
with boundary and corners.
We can moreover perform this construction for a sequence 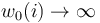 and in each step choose the multi-valued perturbation
and in each step choose the multi-valued perturbation 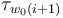 to coincide on
to coincide on 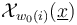 with the (already transverse on these components) perturbation
with the (already transverse on these components) perturbation 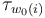 .
Then the required perturbation
.
Then the required perturbation 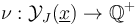 can be obtained as the limit
can be obtained as the limit
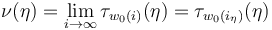 , where
, where 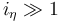 such that
such that 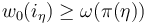 .
.
Construction of Composition Operations
For the Composition Operators in the Polyfold Constructions for Fukaya Categories to be well defined we need to check that 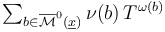 defines an element in the Novikov ring. This requires the following two properties of the perturbed solution sets:
defines an element in the Novikov ring. This requires the following two properties of the perturbed solution sets:
Every perturbed solution 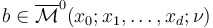 needs to have nonnegative symplectic area
needs to have nonnegative symplectic area 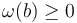 . This is achieved as follows:
. This is achieved as follows:
If all Lagrangians involved are pairwise either identical or transverse, then no Hamiltonian perturbations to the Cauchy-Riemann equation are involved in the construction of the unperturbed moduli space 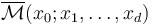 . Thus each component
. Thus each component 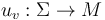 of an unperturbed solution satisfies
of an unperturbed solution satisfies
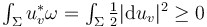 , and this sums up to
, and this sums up to 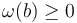 .
Thus the Cauchy-Riemann operator
.
Thus the Cauchy-Riemann operator 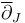 has no zeros in the connected components
has no zeros in the connected components 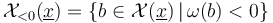 of negative symplectic area. Since transversality is a condition only at solutions, this means we can fix the perturbation
of negative symplectic area. Since transversality is a condition only at solutions, this means we can fix the perturbation 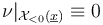 an the connected components of the ambient space of negative energy. As a result, all perturbed solutions will satisfy
an the connected components of the ambient space of negative energy. As a result, all perturbed solutions will satisfy 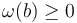 , as required.
, as required.
Here input from the Mirror Symmetry community is needed
on how to define 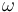 , or which kind of Novikov coefficients to use, in the presence of Hamiltonian perturbations for nontransverse pairs of nonidentical Lagrangians.
, or which kind of Novikov coefficients to use, in the presence of Hamiltonian perturbations for nontransverse pairs of nonidentical Lagrangians.
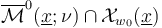 of Fredholm index
of Fredholm index 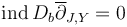 and bounded energy
and bounded energy 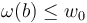 for some
for some 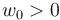 needs to be a finite set.
This is true by the following:
needs to be a finite set.
This is true by the following:
First, the implicit function theorem for transverse sc-Fredholm multi-sections of polyfold bundles implies that the set of perturbed solutions of Fredholm index 0, 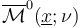 carries the structure of a 0-dimensional weighted-branched orbifold
carries the structure of a 0-dimensional weighted-branched orbifold
WORK IN PROGRESS
CAUTION: need to divide by order of isotropy to get weight functions ?!?
Proof of  -relations
-relations
we need to explain how to obtain regularizations 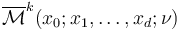 for expected dimensions
for expected dimensions 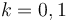 by a choice of perturbations
by a choice of perturbations  .
Moreover, we need to choose these perturbations coherently to ensure that the boundary of each 1-dimensional part is given by Cartesian products of 0-dimensional parts,
.
Moreover, we need to choose these perturbations coherently to ensure that the boundary of each 1-dimensional part is given by Cartesian products of 0-dimensional parts,
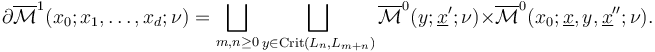
Finally, we need to check that for each pair 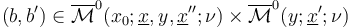 ,
when considered as boundary point
,
when considered as boundary point 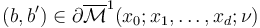 , has symplectic area
, has symplectic area  and weight function
and weight function 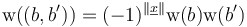 .
.
Analysis TODO:
when degenerating polygons to create a strip withboundary conditions, will need to transfer from Morse-Bott breaking to boundary node