Difference between revisions of "Regularized moduli spaces"
From Polyfolds.org
m |
|||
| Line 20: | Line 20: | ||
Finally, we need to check that for each pair <math>(b,b')\in\overline\mathcal{M}^0(x_0;\underline{x},y,\underline{x}'';\nu)\times\overline\mathcal{M}^0(y;\underline{x}';\nu)</math>, | Finally, we need to check that for each pair <math>(b,b')\in\overline\mathcal{M}^0(x_0;\underline{x},y,\underline{x}'';\nu)\times\overline\mathcal{M}^0(y;\underline{x}';\nu)</math>, | ||
| − | when considered as boundary point <math>(b,b')\in\partial \overline\mathcal{M}^1(x_0;x_1,\ldots,x_d;\nu)</math> has symplectic area <math>\omega((b,b')) = \omega(b) + \omega(b')</math> and weight function <math>\text{w}((b,b')) = (-1)^{\|\underline x\|} \text{w}(b) \text{w}(b')</math>. | + | when considered as boundary point <math>(b,b')\in\partial \overline\mathcal{M}^1(x_0;x_1,\ldots,x_d;\nu)</math>, has symplectic area <math>\omega((b,b')) = \omega(b) + \omega(b')</math> and weight function <math>\text{w}((b,b')) = (-1)^{\|\underline x\|} \text{w}(b) \text{w}(b')</math>. |
Revision as of 18:49, 26 May 2017
Given the moduli spaces of pseudoholomorphic polygons 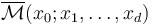 for each tuple of Lagrangians
for each tuple of Lagrangians 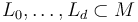 , generators
, generators 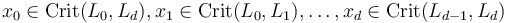 , and a fixed compatible almost complex structure
, and a fixed compatible almost complex structure 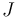 , we need to explain how to obtain regularizations
, we need to explain how to obtain regularizations 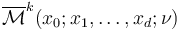 for expected dimensions
for expected dimensions 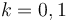 by a choice of perturbations
by a choice of perturbations 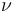 .
Moreover, we need to choose these perturbations coherently to ensure that the boundary of each 1-dimensional part is given by Cartesian products of 0-dimensional parts,
.
Moreover, we need to choose these perturbations coherently to ensure that the boundary of each 1-dimensional part is given by Cartesian products of 0-dimensional parts,
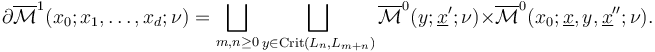
TODO
Finally, we need to check that for each pair 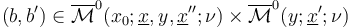 ,
when considered as boundary point
,
when considered as boundary point 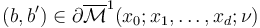 , has symplectic area
, has symplectic area  and weight function
and weight function 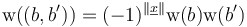 .
.