Difference between revisions of "Gluing construction for Hamiltonians"
From Polyfolds.org
m |
m |
||
| Line 13: | Line 13: | ||
* The Hamiltonian perturbations <math>Y_v</math> should be cut off to vanish outside of the thin parts of the domains <math>\Sigma_v</math>. However, there may be thin parts of a surface <math>\Sigma_v</math> that are not neighborhoods of a puncture. On these, we must choose the Hamiltonian-vector-field-valued one-form <math>Y_v</math> compatible with gluing as in [[http://www.ems-ph.org/books/book.php?proj_nr=12 Seidel book]]. | * The Hamiltonian perturbations <math>Y_v</math> should be cut off to vanish outside of the thin parts of the domains <math>\Sigma_v</math>. However, there may be thin parts of a surface <math>\Sigma_v</math> that are not neighborhoods of a puncture. On these, we must choose the Hamiltonian-vector-field-valued one-form <math>Y_v</math> compatible with gluing as in [[http://www.ems-ph.org/books/book.php?proj_nr=12 Seidel book]]. | ||
| − | * For example, in the neighbourhood of a tree with an edge <math>e=(v,w)</math> between main vertices, there are trees in which this edge is removed, the two vertices are replaced by a single vertex <math>v\#w</math>, and the surfaces <math>\Sigma_v,\Sigma_w</math> are replaced by a single [[glued surface]] (or find reference in [[Deligne-Mumford | + | * For example, in the neighbourhood of a tree with an edge <math>e=(v,w)</math> between main vertices, there are trees in which this edge is removed, the two vertices are replaced by a single vertex <math>v\#w</math>, and the surfaces <math>\Sigma_v,\Sigma_w</math> are replaced by a single [[glued surface]] (or find reference in [[Deligne-Mumford space]]) <math>\Sigma_{v\#w}=\Sigma_v \#_R \Sigma_w</math> for <math>R\gg 1</math>. Compatibility with gluing requires that the Hamiltonian perturbation on these glued surfaces is also given by a gluing construction <math>Y_{v\#w}=Y_v \#_R Y_w</math> (in which the two perturbations <math>Y_v,Y_w</math> agree and hence can be matched over a long neck <math>[-R,R]\times[0,1]\subset \Sigma_{v\#w}</math>). |
Latest revision as of 20:43, 7 June 2017
TODO: As cited in [expansion of expansion in point 7], construct vector-field-valued 1-forms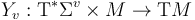 
on 
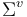compatibly with the fixed Hamiltonian perturbations.
Copies from moduli spaces of pseudoholomorphic polygons:
- On the thin part
![\iota _{e}^{v}:[0,\infty )\times [0,1]\hookrightarrow \Sigma ^{v}](/images/math/d/1/1/d1100c1e7510c1014aac509f6b8fd6de.png)
near each puncture 
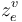we have 
.
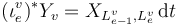- Note that this convention together with our symmetric choice of Hamiltonian perturbations
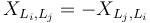forces the vector-field-valued 1-form on ![\Sigma ^{v}\simeq \mathbb{R} \times [0,1]](/images/math/5/6/a/56a3486ce4c38533929719c2fae3d318.png)
in cas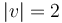e 
to be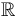 
-invariant, 
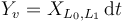if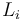 
are the Lagrangian labels for the boundary components 
.
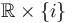- Here and in the following we denote
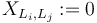in case 
, so that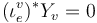 
in case 
.
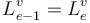- The Hamiltonian perturbations
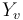should be cut off to vanish outside of the thin parts of the domains 
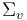. However, there may be thin parts of a surface 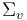that are not neighborhoods of a puncture. On these, we must choose the Hamiltonian-vector-field-valued one-form 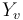compatible with gluing as in [Seidel book].
- For example, in the neighbourhood of a tree with an edge
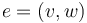between main vertices, there are trees in which this edge is removed, the two vertices are replaced by a single vertex 
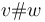, and the surfaces 
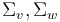are replaced by a single glued surface (or find reference in Deligne-Mumford space) 
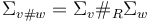for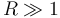 
. Compatibility with gluing requires that the Hamiltonian perturbation on these glued surfaces is also given by a gluing construction 
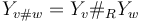(in which the two perturbations 
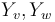agree and hence can be matched over a long neck ![[-R,R]\times [0,1]\subset \Sigma _{{v\#w}}](/images/math/7/c/1/7c10420071147771af7f4f746f0fc075.png)
).
