Some retraction problems
Contents
A useful toy retraction
Fix a non-negative function 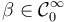 for which
for which 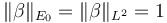 .
We consider the sc-Banach space
.
We consider the sc-Banach space 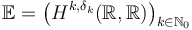 with
with 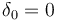 .
Define a family of linear projections
.
Define a family of linear projections 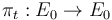 for
for 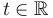 by
by 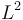 -projection onto the subspace spanned by
-projection onto the subspace spanned by 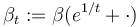 for
for 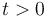 respectively
respectively 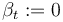 for
for 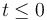 .
The corresponding retraction
.
The corresponding retraction
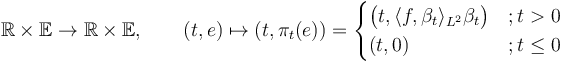
is sc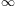 (see Lemma 1.23 in the HWZ sc-smoothness paper)) and a retraction (in fact, a splicing).
(see Lemma 1.23 in the HWZ sc-smoothness paper)) and a retraction (in fact, a splicing).
Question: What is the sc-retract of this sc-smooth retraction? Describe this space (somewhat) geometrically.
Question: Find a subset of 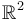 homeomorphic to this sc-retract. Hint: It will contain the line
homeomorphic to this sc-retract. Hint: It will contain the line 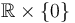 .
.
Question: Which paths of the form 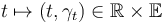 are contained in the sc-retract and are sc-smooth? Can these paths be described via the above homeomorphism of the retract to
are contained in the sc-retract and are sc-smooth? Can these paths be described via the above homeomorphism of the retract to 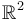 ?
?
Question: What is the tangent fiber of the sc-retract at the point 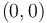 ? Can all points in this fiber be achieved as tangent vectors to paths in the retract passing through
? Can all points in this fiber be achieved as tangent vectors to paths in the retract passing through 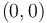 ? Is the tangent vector at
? Is the tangent vector at 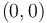 of a path in the sc-retract always contained in the tangent fiber of the retract at
of a path in the sc-retract always contained in the tangent fiber of the retract at 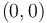 ?
?
Independence of choice of retraction
Let 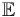 be some sc-Banach space, and suppose
be some sc-Banach space, and suppose 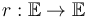 is an sc-smooth retraction, with
is an sc-smooth retraction, with 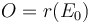 .
.
The model lemmas
Retractions instead of sc-Banach manifolds
1. Transversal constraint construction as retraction
2. Target manifold as 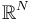 3. Retractions on retracts
4. Does smoothness depend on choice of retraction?
3. Retractions on retracts
4. Does smoothness depend on choice of retraction?