Difference between revisions of "Some retraction problems"

Revision as of 08:37, 12 June 2017

Scale calculus was developed to make reparametrization actions on function spaces smooth. All the key issues and ideas can already be seen at the example of 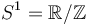$S^{1}=\mathbb{R} /\mathbb{Z }$ acting on a space of nonconstant functions on 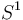$S^{1}$ , for example the shift action

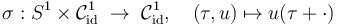
$\sigma :S^{1}\times {\mathcal {C}}_{{{\rm {id}}}}^{1}\;\to \;{\mathcal {C}}_{{{\rm {id}}}}^{1},\quad (\tau ,u)\mapsto u(\tau +\cdot )$

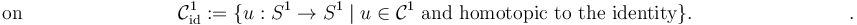
${\text{on}}\qquad \qquad \qquad \qquad {\mathcal {C}}_{{{\rm {id}}}}^{1}:=\{u:S^{1}\to S^{1}\;|\;u\in {\mathcal {C}}^{1}\;{\text{and homotopic to the identity}}\}.\qquad \qquad \qquad \qquad .$

The purpose of the following exercises is to give the quotient of S^1-valued functions homotopic to the identity, modulo reparametrization by shifts, 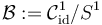${\mathcal {B}}:={\mathcal {C}}_{{{\rm {id}}}}^{1}/S^{1}$ the structure of a scale-smooth manifold ... and to see that classical Banach space topologies fail at giving it a differentiable Banach manifold structure.

differentiability of shift map

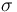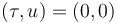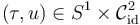Compute the directional derivatives of the shift map $\sigma$ , first at $(\tau ,u)=(0,0)$ , then at $(\tau ,u)\in S^{1}\times {\mathcal {C}}_{{{\rm {id}}}}^{2}$ .

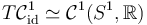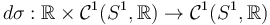Next, understand how to identify $T{\mathcal {C}}_{{{\rm {id}}}}^{1}\simeq {\mathcal {C}}^{1}(S^{1},\mathbb{R} )$ , and write down a conjectural formula for the differential $d\sigma :\mathbb{R} \times {\mathcal {C}}^{1}(S^{1},\mathbb{R} )\to {\mathcal {C}}^{1}(S^{1},\mathbb{R} )$ .

Then recall the definition of differentiability in terms of uniform linear approximation and see whether it can be satisfied at any base point 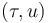$(\tau ,u)$ .

YOUR SOLUTION WANTS TO BE HERE

local charts

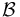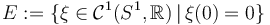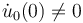Verify that ${\mathcal {B}}$ has local Banach manifold charts modeled on $E:=\{\xi \in {\mathcal {C}}^{1}(S^{1},\mathbb{R} )\,|\,\xi (0)=0\}$ . To set up a chart near a given point, pick a representative $[u_{0}]\in {\mathcal {B}}$ with ${\dot u}_{0}(0)\neq 0$ and consider the map