Scale calculus problems
Scale calculus was developed to make reparametrization actions on function spaces smooth.
All the key issues and ideas can already be seen at the example of 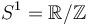 acting on a space of nonconstant functions on
acting on a space of nonconstant functions on 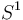 , for example the shift action
, for example the shift action
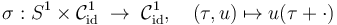
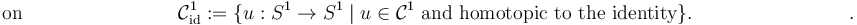
The purpose of the following exercises is to give the quotient of S^1-valued functions homotopic to the identity, modulo reparametrization by shifts,
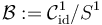 the structure of a scale-smooth manifold ... and to see that classical Banach space topologies fail at giving it a differentiable Banach manifold structure.
the structure of a scale-smooth manifold ... and to see that classical Banach space topologies fail at giving it a differentiable Banach manifold structure.
Contents
differentiability of shift map
Compute the directional derivatives of the shift map 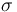 ,
first at
,
first at 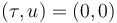 , then at
, then at 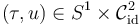 .
.
Next, understand how to identify 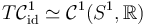 ,
and write down a conjectural formula for the differential
,
and write down a conjectural formula for the differential 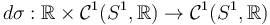 .
.
Then recall the definition of differentiability in terms of uniform linear approximation and see whether it can be satisfied at any base point 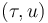 .
.
solution
local charts
Verify that 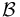 has local Banach manifold charts modeled on
has local Banach manifold charts modeled on
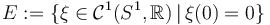 .
To set up a chart near a given point, pick a representative
.
To set up a chart near a given point, pick a representative ![[u_{0}]\in {\mathcal {B}}](/images/math/a/7/5/a75d0ef61aeba62f7c4cec102ef3ffe1.png) with
with 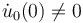 and consider
and consider
Failed to parse (syntax error): \phi_{u_0}: \{\xi\in E\,|\, \|\xi\|_{\mathcal{C}^1<\epsilon \} \to \mathcal{B} , \qquad \xi \mapsto [u_0+\xi] .
solution
transition maps
For ![[u_{0}]=[u_{1}]\in {\mathcal {B}}](/images/math/7/c/e/7ceed67f126cbf1b004ab2026e9e8fc7.png) with representatives
with representatives 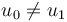 but
but 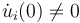 determine the
transition map
determine the
transition map 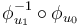 .
.
Then find an example of a point and direction in which this transition map is not differentiable.
solution
alternative Banach norms
solution
Show that the shift action 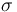 of #homework 7 is a scale-smooth map by the following steps:
of #homework 7 is a scale-smooth map by the following steps:
a) find a scale-Banach space 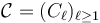 with
with 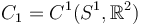
b) show that 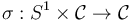 is
is 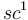 and calculate
and calculate 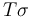
c) iteratively show that 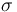 is
is 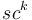 for all k
for all k
Note: The actual map in #homework 7 is a restriction of this map here to a submanifold of 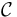 (taking values in
(taking values in 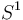 , of fixed degree).
, of fixed degree).