Problems on Fredholm sections of polyfold bundles, perturbations, and implicit function theorems
To simplify notation, we will study the Cauchy-Riemann equation for maps from the torus 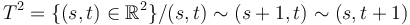
to 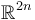 with a nonconstant almost complex structure
with a nonconstant almost complex structure 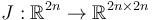 .
.
The advanced versions of the following problems study maps on cylinders
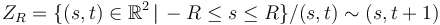 ,
,
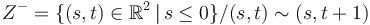 ,
,
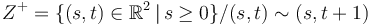 .
.
Contents
- 1 strong scale-smooth bundles
- 2 strong M-polyfold bundles
- 3 regularizing and sections
- 4 sections of M-polyfold bundles
- 5 linear sc-Fredholm property
- 6 linear sc-Fredholm property on M-polyfold
- 7 nonlinear sc-Fredholm property
- 8 nonlinear sc-Fredholm property on M-polyfold
- 9 implicit function theorem
- 10 transverse perturbations
- 11 Invariance
- 12 Compactness
strong scale-smooth bundles
Understand in what sense 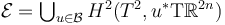 forms a strong bundle over
forms a strong bundle over 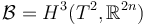 .
.
YOUR SOLUTION WANTS TO BE HERE
strong M-polyfold bundles
Understand in what sense
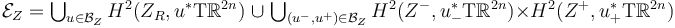
forms a strong bundle over the M-polyfold
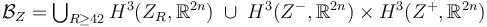
YOUR SOLUTION WANTS TO BE HERE
regularizing and 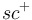 sections
sections
Verify that 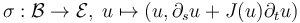 is scale smooth and regularizing but not
is scale smooth and regularizing but not 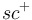 .
.
Then find some examples of 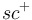 sections of
sections of 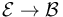 . (Hint: Think about classical geometric perturbations of the Cauchy-Riemann equation.)
. (Hint: Think about classical geometric perturbations of the Cauchy-Riemann equation.)
Are perturbations of the almost complex structure 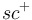 -perturbations of
-perturbations of 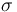 ?
?
YOUR SOLUTION WANTS TO BE HERE
sections of M-polyfold bundles
In what sense is the following section scale-smooth and regularizing?
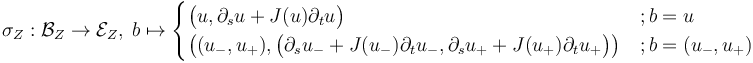
YOUR SOLUTION WANTS TO BE HERE
linear sc-Fredholm property
Compute the linearization of 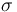 at a constant map
at a constant map 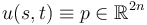 , and show that it is a linear sc-Fredholm operator.
, and show that it is a linear sc-Fredholm operator.
YOUR SOLUTION WANTS TO BE HERE
linear sc-Fredholm property on M-polyfold
Compute the linearization of 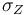 at points
at points 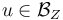 and
and 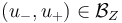 , and show that both are linear sc-Fredholm operators.
, and show that both are linear sc-Fredholm operators.
YOUR SOLUTION WANTS TO BE HERE
nonlinear sc-Fredholm property
Show that 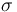 is an sc-Fredholm section. (Hint: Use the fact that it is continuously differentiable, and the linearizations are Fredholm.)
is an sc-Fredholm section. (Hint: Use the fact that it is continuously differentiable, and the linearizations are Fredholm.)
YOUR SOLUTION WANTS TO BE HERE
nonlinear sc-Fredholm property on M-polyfold
Compute the expression for the section 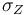 in the M-polyfold and bundle charts arising from plus-minus-(pre)gluing.
in the M-polyfold and bundle charts arising from plus-minus-(pre)gluing.
To simplify the technical setting in the following, restrict 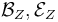 to functions/sections in
to functions/sections in 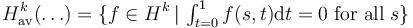 .
.
Then find a filled section for 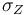 by using the invertible operator
by using the invertible operator 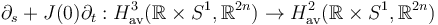 .
.
Finally, sketch out a proof for this filled section being sc-Fredholm.
YOUR SOLUTION WANTS TO BE HERE
implicit function theorem
Explain how the contraction germ form of an sc-Fredholm section is used in the proof that transverse sc-Fredholm sections have a smooth, finite dimensional, zero set.
YOUR SOLUTION WANTS TO BE HERE
transverse perturbations
Suppose that an sc-Fredholm section 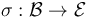 of an M-polyfold bundle (modeled on scale-Hilbert spaces)
is transverse except for a compact subset
of an M-polyfold bundle (modeled on scale-Hilbert spaces)
is transverse except for a compact subset 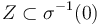 . Then, given any open neighbourhood
. Then, given any open neighbourhood 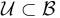 of
of 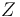 , find a perturbation
, find a perturbation 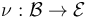 supported in
supported in 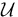 such that
such that 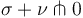 ,
by working through the following steps.
,
by working through the following steps.
(A) For any 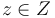 find a stabilization
find a stabilization 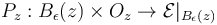 on a neighborhood
on a neighborhood 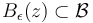 of
of 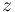 by a finite dimensional vector space
by a finite dimensional vector space 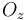 , so that
, so that 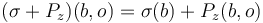 is a transverse section over
is a transverse section over 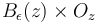 .
.
(B) Use compactness of 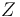 and the existence of smooth cutoff functions (on scale-Hilbert spaces) to construct a global section
and the existence of smooth cutoff functions (on scale-Hilbert spaces) to construct a global section
 that is transverse after stabilization with a finite dimensional vector space
that is transverse after stabilization with a finite dimensional vector space 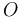 and agrees with
and agrees with 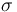 outside of
outside of 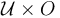 .
.
(C) Explain why 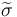 is sc-Fredholm, then apply the polyfold implicit function theorem to it.
is sc-Fredholm, then apply the polyfold implicit function theorem to it.
(D) Use the Sard theorem to find regular values of the projection  , and understand why these yield transverse perturbations of
, and understand why these yield transverse perturbations of 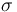 .
(Hint: This is analogous to the universal moduli space approach for finding regular almost complex structures or Hamiltonian perturbations in geometric regularization methods.)
.
(Hint: This is analogous to the universal moduli space approach for finding regular almost complex structures or Hamiltonian perturbations in geometric regularization methods.)
YOUR SOLUTION WANTS TO BE HERE
Invariance
Suppose that 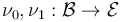 are two transverse perturbations for an sc-Fredholm section
are two transverse perturbations for an sc-Fredholm section 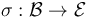 of an M-polyfold bundle (modeled on scale-Hilbert spaces) without boundary or corners.
Explain how to obtain a (not yet necessarily compact) manifold with boundary
of an M-polyfold bundle (modeled on scale-Hilbert spaces) without boundary or corners.
Explain how to obtain a (not yet necessarily compact) manifold with boundary  .
.
YOUR SOLUTION WANTS TO BE HERE
Compactness
Suppose that an sc-Fredholm section 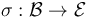 of an M-polyfold bundle has compact zero set.
What can be said about the perturbed zero set
of an M-polyfold bundle has compact zero set.
What can be said about the perturbed zero set 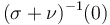 for a scale-smooth perturbation
for a scale-smooth perturbation 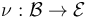 if
if
-
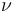 is small in the sense that
is small in the sense that 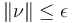 for some norm
for some norm 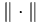 on the fibers of
on the fibers of 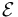 ?
?
-
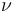 is supported in a small neighborhood of
is supported in a small neighborhood of 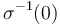 ?
?
Then understand how the 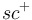 property of a perturbation
property of a perturbation 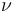 , together with boundedness in an auxiliary norm, and smallness in the second sense, can guarantee compactness of the perturbed zero set
, together with boundedness in an auxiliary norm, and smallness in the second sense, can guarantee compactness of the perturbed zero set 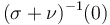 .
.
YOUR SOLUTION WANTS TO BE HERE