Problems on Fredholm sections of polyfold bundles, perturbations, and implicit function theorems
To simplify notation, we will study the Cauchy-Riemann equation for maps from the torus 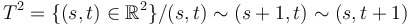
to 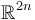 with a nonconstant almost complex structure
with a nonconstant almost complex structure 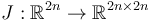 .
.
The advanced versions of the following problems study maps on cylinders
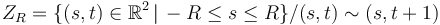 ,
,
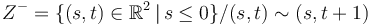 ,
,
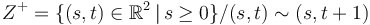 .
.
Contents
- 1 strong scale-smooth bundles
- 2 strong M-polyfold bundles
- 3 regularizing and sections
- 4 sections of M-polyfold bundles
- 5 linear sc-Fredholm property
- 6 linear sc-Fredholm property on M-polyfold
- 7 nonlinear sc-Fredholm property
- 8 nonlinear sc-Fredholm property on M-polyfold
- 9 implicit function theorem
- 10 transverse perturbations
- 11
- 12
- 13
- 14
strong scale-smooth bundles
Understand in what sense 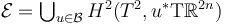 forms a strong bundle over
forms a strong bundle over 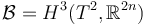 .
.
YOUR SOLUTION WANTS TO BE HERE
strong M-polyfold bundles
Understand in what sense
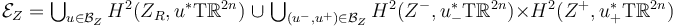
forms a strong bundle over the M-polyfold
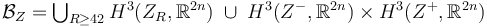
YOUR SOLUTION WANTS TO BE HERE
regularizing and 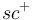 sections
sections
Verify that 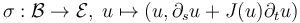 is scale smooth and regularizing but not
is scale smooth and regularizing but not 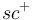 .
.
Then find some examples of 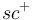 sections of
sections of 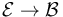 . (Hint: Think about classical geometric perturbations of the Cauchy-Riemann equation.)
. (Hint: Think about classical geometric perturbations of the Cauchy-Riemann equation.)
Are perturbations of the almost complex structure 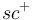 -perturbations of
-perturbations of 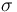 ?
?
YOUR SOLUTION WANTS TO BE HERE
sections of M-polyfold bundles
In what sense is the following section scale-smooth and regularizing?
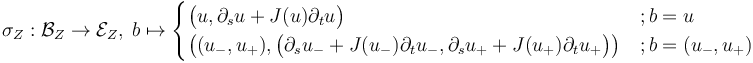
YOUR SOLUTION WANTS TO BE HERE
linear sc-Fredholm property
Compute the linearization of 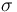 at a constant map
at a constant map 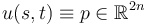 , and show that it is a linear sc-Fredholm operator.
, and show that it is a linear sc-Fredholm operator.
YOUR SOLUTION WANTS TO BE HERE
linear sc-Fredholm property on M-polyfold
Compute the linearization of 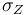 at points
at points 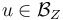 and
and 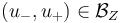 , and show that both are linear sc-Fredholm operators.
, and show that both are linear sc-Fredholm operators.
YOUR SOLUTION WANTS TO BE HERE
nonlinear sc-Fredholm property
Show that 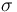 is an sc-Fredholm section. (Hint: Use the fact that it is continuously differentiable, and the linearizations are Fredholm.)
is an sc-Fredholm section. (Hint: Use the fact that it is continuously differentiable, and the linearizations are Fredholm.)
YOUR SOLUTION WANTS TO BE HERE
nonlinear sc-Fredholm property on M-polyfold
Compute the expression for the section 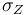 in the M-polyfold and bundle charts arising from plus-minus-(pre)gluing.
in the M-polyfold and bundle charts arising from plus-minus-(pre)gluing.
To simplify the technical setting in the following, restrict 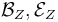 to functions/sections in
to functions/sections in 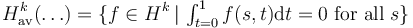 .
.
Then find a filled section for 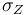 by using the invertible operator
by using the invertible operator 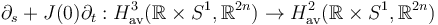 .
.
Finally, sketch out a proof for this filled section being sc-Fredholm.
YOUR SOLUTION WANTS TO BE HERE
implicit function theorem
Explain how the contraction germ form of an sc-Fredholm section is used in the proof that transverse sc-Fredholm sections have a smooth, finite dimensional, zero set.
YOUR SOLUTION WANTS TO BE HERE
transverse perturbations
Suppose that an sc-Fredholm section 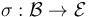 of an M-polyfold bundle (modeled on scale-Hilbert spaces)
is transverse except for a compact subset
of an M-polyfold bundle (modeled on scale-Hilbert spaces)
is transverse except for a compact subset 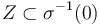 . Then, given any open neighbourhood Failed to parse (unknown function "\matcal"): \matcal{U}\subset\mathcal{B}
. Then, given any open neighbourhood Failed to parse (unknown function "\matcal"): \matcal{U}\subset\mathcal{B}
of, find a perturbation
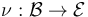 supported in Failed to parse (unknown function "\matcal"): \matcal{U}
supported in Failed to parse (unknown function "\matcal"): \matcal{U}
such that,
by working through the following steps.
- For any
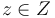 find a stabilization Failed to parse (syntax error): P_z: B_\epsilon(z) \times O_z \to \mathcal{E}|_{B_\epsilon(z)
find a stabilization Failed to parse (syntax error): P_z: B_\epsilon(z) \times O_z \to \mathcal{E}|_{B_\epsilon(z)
on a neighborhoodof
by a finite dimensional vector space
,
so that 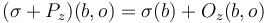 is a transverse section over
is a transverse section over 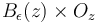 .
.
- Use compactness of
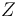 and the existence of smooth cutoff functions (on scale-Hilbert spaces) to construct a global section
and the existence of smooth cutoff functions (on scale-Hilbert spaces) to construct a global section
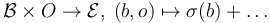 that is transverse after stabilization with a finite dimensional vector space
that is transverse after stabilization with a finite dimensional vector space 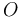 .
.
YOUR SOLUTION WANTS TO BE HERE
YOUR SOLUTION WANTS TO BE HERE
YOUR SOLUTION WANTS TO BE HERE
YOUR SOLUTION WANTS TO BE HERE
YOUR SOLUTION WANTS TO BE HERE