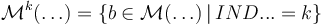Moduli spaces of pseudoholomorphic polygons
To construct the moduli spaces from which the composition maps are defined we fix an auxiliary almost complex structure 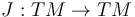 which is compatible with the symplectic structure in the sense that
which is compatible with the symplectic structure in the sense that 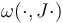 defines a metric on
defines a metric on 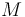 . (Unless otherwise specified, we will use this metric in all following constructions.)
Then given Lagrangians
. (Unless otherwise specified, we will use this metric in all following constructions.)
Then given Lagrangians 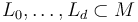 and generators
and generators 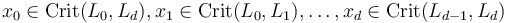 of their morphism spaces, we need to specify the (compactified) moduli space
of their morphism spaces, we need to specify the (compactified) moduli space 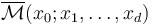 .
We will do this by combining two special cases which we discuss first.
.
We will do this by combining two special cases which we discuss first.
Pseudoholomorphic polygons for pairwise transverse Lagrangians
If each consecutive pair of Lagrangians is transverse, i.e. 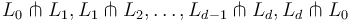 , then our construction is based on pseudoholomorphic polygons
, then our construction is based on pseudoholomorphic polygons
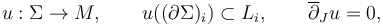
where 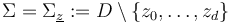 is a disk with
is a disk with 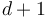 boundary punctures in counter-clockwise order
boundary punctures in counter-clockwise order 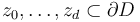 , and
, and 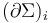 denotes the boundary component between
denotes the boundary component between 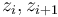 (resp. between
(resp. between 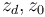 for i=d).
More precisely, we construct the (uncompactified) moduli spaces of pseudoholomorphic polygons for any tuple
for i=d).
More precisely, we construct the (uncompactified) moduli spaces of pseudoholomorphic polygons for any tuple 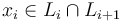 for
for 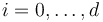 as in [S]:
as in [S]:
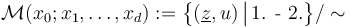
where
-
 is a tuple of pairwise disjoint marked points on the boundary of a disk, in counter-clockwise order.
is a tuple of pairwise disjoint marked points on the boundary of a disk, in counter-clockwise order. -
 is a smooth map satisfying
is a smooth map satisfying
- the Cauchy-Riemann equation
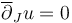 ,
, - Lagrangian boundary conditions
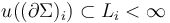 ,
, - the finite energy condition
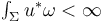 ,
, - the limit conditions
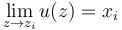 for
for  .
.
- the Cauchy-Riemann equation
Here two pseudoholomorphic polygons are equivalent 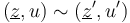 if there is a disk automorphism
if there is a disk automorphism 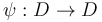 that preserves the complex structure on
that preserves the complex structure on 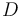 , the marked points
, the marked points 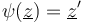 , and relates the pseudoholomorphic polygons by reparametrization,
, and relates the pseudoholomorphic polygons by reparametrization, 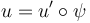 .
.
For 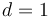 , the twice punctured disks are all biholomorphic to the strip
, the twice punctured disks are all biholomorphic to the strip ![\Sigma _{{\{z_{0},z_{1}\}}}\simeq \mathbb{R} \times [0,1]](/images/math/8/b/3/8b3c9f4dfa661a678858f5301011005f.png) , so that we could equivalently set up the moduli spaces
, so that we could equivalently set up the moduli spaces 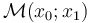 by fixing the domain
by fixing the domain ![\Sigma _{{d=1}}:=\mathbb{R} \times [0,1]](/images/math/b/9/b/b9b8b4c742fe7b67774c1dfe2eb02833.png) and defining the equivalence relation
and defining the equivalence relation 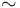 only in terms of the shift action
only in terms of the shift action 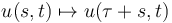 of
of 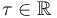 .
.
For 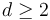 , the moduli space of domains
, the moduli space of domains
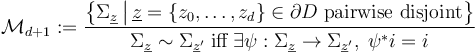
can be compactified to form the Deligne-Mumford space 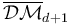 , whose boundary and corner strata can be represented by trees of polygonal domains
, whose boundary and corner strata can be represented by trees of polygonal domains 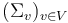 with each edge
with each edge 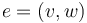 represented by two punctures
represented by two punctures 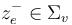 and
and 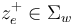 . The thin neighbourhoods of these punctures are biholomorphic to half-strips, and then a neighbourhood of a tree of polygonal domains is obtained by gluing the domains together at the pairs of strip-like ends represented by the edges.
. The thin neighbourhoods of these punctures are biholomorphic to half-strips, and then a neighbourhood of a tree of polygonal domains is obtained by gluing the domains together at the pairs of strip-like ends represented by the edges.
compactified moduli spaces
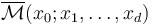
Pseudoholomorphic disk trees for a fixed Lagrangian
If the Lagrangians are all the same,  , then our construction is based on pseudoholomorphic disks
, then our construction is based on pseudoholomorphic disks
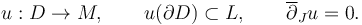
For a sequence of such maps (modulo reparametrization by automorphisms of the disk), energy concentration at a boundary point is usually captured in terms of a disk bubble attached via a boundary node. This yields to a compactification of the moduli space of pseudoholomorphic disks modulo reparametrization that is given by adding boundary strata consisting of fiber products of moduli spaces of disks.
One could - as in the approach by Fukaya et al - regularize such a space and then interpret disk bubbling as contribution to 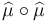 - where the composition is via a push-pull construction on some space of chains, currents, or differential forms on the Lagrangian. However, such push-pull constructions require transversality of the chains to the evaluation maps from the regularized moduli spaces, so that a rigorous construction of the
- where the composition is via a push-pull construction on some space of chains, currents, or differential forms on the Lagrangian. However, such push-pull constructions require transversality of the chains to the evaluation maps from the regularized moduli spaces, so that a rigorous construction of the 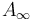 -structure in this setting requires a complicated infinite iteration.
-structure in this setting requires a complicated infinite iteration.
We will resolve this issue as in [JL] by following another earlier proposal by Fukaya-Oh to allow disks to flow apart along a Morse trajectory.
Here we work throughout with the Morse function 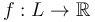 chosen in the setup of the morphism space
chosen in the setup of the morphism space 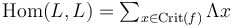 . We also choose a metric on
. We also choose a metric on 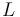 so that the gradient vector field
so that the gradient vector field 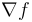 satisfies the Morse-Smale conditions and an additional technical assumption in [1] which guarantees a natural smooth manifold-with-boundary-and-corners structure on the compactified Morse trajectory spaces
satisfies the Morse-Smale conditions and an additional technical assumption in [1] which guarantees a natural smooth manifold-with-boundary-and-corners structure on the compactified Morse trajectory spaces
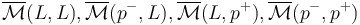 for
for 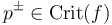 .
This smooth structure is essentially induced by the requirement that the evaluation maps at positive and negative ends
.
This smooth structure is essentially induced by the requirement that the evaluation maps at positive and negative ends 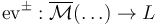 are smooth.
With that data and the fixed almost complex structure
are smooth.
With that data and the fixed almost complex structure 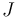 we can construct the moduli spaces of pseudoholomorphic disk trees for any tuple
we can construct the moduli spaces of pseudoholomorphic disk trees for any tuple 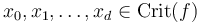 as in JL:
as in JL:
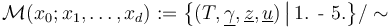
where
-
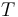 is an ordered tree with the following structure on the sets of vertices
is an ordered tree with the following structure on the sets of vertices 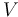 and edges
and edges 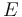 :
:
- The edges
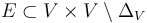 are oriented towards the root vertex
are oriented towards the root vertex 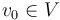 of the tree, i.e. for
of the tree, i.e. for 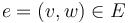 the outgoing vertex
the outgoing vertex 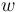 is still connected to the root after removing
is still connected to the root after removing 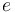 . Thus each vertex
. Thus each vertex 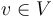 has a unique outgoing edge
has a unique outgoing edge 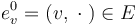 and a (possibly empty) set of incoming edges
and a (possibly empty) set of incoming edges 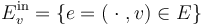 . Moreover, the set of incoming edges is ordered,
. Moreover, the set of incoming edges is ordered, 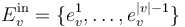 with
with 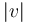 denoting the valence - number of attached edges - of
denoting the valence - number of attached edges - of 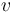 ).
). - The set of vertices is partitioned
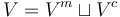 into the sets of main vertices
into the sets of main vertices 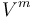 and the set of critical vertices
and the set of critical vertices 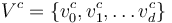 . The latter is ordered to start with the root
. The latter is ordered to start with the root 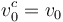 , which is required to have a single edge
, which is required to have a single edge 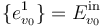 , and then contains d leaves
, and then contains d leaves 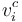 of the tree (i.e. with
of the tree (i.e. with 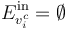 ), with order induced by the orientation and order of the edges (with the root being the minimal vertex).
), with order induced by the orientation and order of the edges (with the root being the minimal vertex).
- The edges
-
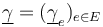 is a tuple of generalized Morse trajectories in the following compactified Morse trajectory spaces:
is a tuple of generalized Morse trajectories in the following compactified Morse trajectory spaces:
-
 for any edge
for any edge 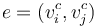 between critical vertices;
between critical vertices; 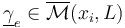 for any edge
for any edge 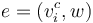 from a critical vertex
from a critical vertex 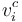 to a main vertex
to a main vertex  ;
;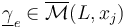 for any edge
for any edge 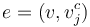 from a main vertex
from a main vertex 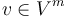 to a critical vertex
to a critical vertex 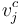 ;
;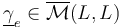 for any edge
for any edge 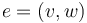 between main vertices
between main vertices 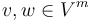 .
.
-
-
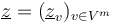 is a tuple of boundary marked points as follows:
is a tuple of boundary marked points as follows:
- For each main vertex
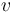 there are
there are 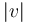 pairwise disjoint marked points
pairwise disjoint marked points 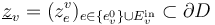 on the boundary of a disk.
on the boundary of a disk. - The order
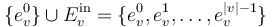 of the edges corresponds to a counter-clockwise order of the marked points
of the edges corresponds to a counter-clockwise order of the marked points 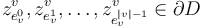 .
. - The marked points can also be denoted as
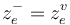 and
and 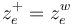 by the edges
by the edges 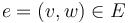 for which
for which 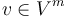 or
or  .
.
- For each main vertex
- For each main vertex
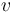 there is a pseudoholomorphic disk, that is a smooth map
there is a pseudoholomorphic disk, that is a smooth map 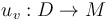 satisfying
satisfying
- the Cauchy-Riemann equation
 ,
, - Lagrangian boundary conditions
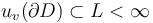 ,
, - the finite energy condition
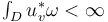 .
. - The pseudholomorphic disks can also be indexed as
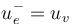 and
and 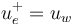 by the edges
by the edges 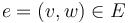 for which
for which 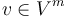 or
or  . In that notation, they satisfy the matching conditions with the generalized Morse trajectories
. In that notation, they satisfy the matching conditions with the generalized Morse trajectories 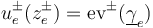 whenever
whenever 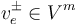 .
.
- the Cauchy-Riemann equation
- The disk tree is stable in the sense that any main vertex
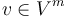 whose disk has zero energy
whose disk has zero energy 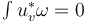 (which is equivalent to
(which is equivalent to 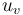 being constant) has valence
being constant) has valence 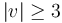 .
.
Finally, two pseudoholomorphic disk trees are equivalent 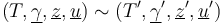 if there is a tree isomorphism
if there is a tree isomorphism 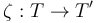 and a tuple of disk automorphisms
and a tuple of disk automorphisms 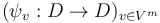 preserving the complex structure on
preserving the complex structure on 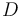 such that
such that
- T preserves the tree structure and order of edges;
- the Morse trajectories are the preserved
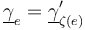 for every
for every 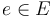 ;
; - the marked points are preserved
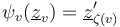 for every
for every 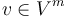 ;
; - the pseudoholomorphic disks are related by reparametrization,
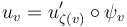 for every
for every 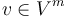 .
.
TODO: if J with no spheres, then compact and trivial isotropy [JL,Prop.2.5]
... otherwise add spheres as below and gnerally nontrivial isotropy
General moduli space of pseudoholomorphic polygons
Make up for differences in Hamiltonian symplectomorphisms applied to each Lagrangian by a domain-dependent Hamiltonian perturbation to the Cauchy-Riemann equation
Finally, the symplectic area function 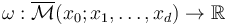 in each case is given by TODO
in each case is given by TODO
Fredholm index