Difference between revisions of "Global Polyfold Fredholm setup"
Natebottman (Talk | contribs) |
Natebottman (Talk | contribs) |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== EP-groupoid basics == | == EP-groupoid basics == | ||
| + | A polyfold should be an "M-polyfold with isotropy". | ||
| + | This is implemented via the language of EP-groupoids, which in finite dimensions reduce to orbifolds. | ||
| + | First, recall that a '''groupoid''' is a small category in which every morphism is invertible (hence a groupoid with a single object is the same thing as a group). | ||
| + | Now define an '''EP-groupoid''' to be a groupoid <math>X</math> with morphism set <math>\mathbf X</math> satisfying these properties: | ||
| + | * '''(Lie):''' <math>X</math> and <math>\mathbf X</math> are equipped with M-polyfold structures, with respect to which the source, target, multiplication, unit, and inversion maps | ||
| + | <center><math> | ||
| + | s: \mathbf X \to X, \quad t: \mathbf X \to X, \quad m: \mathbf X {}_s\times_t \mathbf X \to X, \quad u: X \to \mathbf X, \quad i: \mathbf X \to \mathbf X | ||
| + | </math></center> | ||
| + | are sc-smooth. | ||
| + | * '''(etale):''' <math>s</math> and <math>t</math> are surjective local sc-diffeomorphisms. | ||
| + | * '''(proper):''' For every <math>x \in X</math>, there exists a neighborhood <math>V(x)</math> so that <math>t: s^{-1}\bigl(\overline{V(x)}\bigr) \to X</math> is proper. | ||
| + | Note that '''(Lie)''' makes sense because '''(etale)''' hypothesis implies that <math>\mathbf X {}_s\times_t \mathbf X</math> inherits an M-polyfold structure. | ||
| + | Moreover, '''(proper)''' implies that each isotropy group <math>\mathbf G(x) := \{g \;|\; s(g) = t(g) = x\}</math> is finite. | ||
| + | We denote the orbit space by <math>|X|</math>. | ||
| + | A '''polyfold structure''' on a (paracompact, Hausdorff) space <math>Z</math> is simply <math>(X,\beta)</math> where <math>X</math> is an EP-groupoid and <math>\beta: |X| \to Z</math> is a homeomorphism. | ||
| + | |||
| + | We now illustrate the concept of an EP-groupoid in the following | ||
<div class="toccolours mw-collapsible mw-collapsed"> | <div class="toccolours mw-collapsible mw-collapsed"> | ||
| − | '''Example''': | + | '''Example''': the EP-groupoid structure of <math>DM(1,2)</math>. |
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
blah blah | blah blah | ||
</div></div> | </div></div> | ||
Latest revision as of 10:16, 3 June 2017
EP-groupoid basics
A polyfold should be an "M-polyfold with isotropy".
This is implemented via the language of EP-groupoids, which in finite dimensions reduce to orbifolds.
First, recall that a groupoid is a small category in which every morphism is invertible (hence a groupoid with a single object is the same thing as a group).
Now define an EP-groupoid to be a groupoid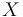 
with morphism set 
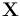satisfying these properties:
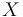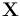- (Lie): and are equipped with M-polyfold structures, with respect to which the source, target, multiplication, unit, and inversion maps
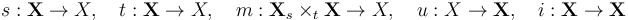
are sc-smooth.
- (etale):
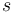and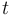 
are surjective local sc-diffeomorphisms. - (proper): For every
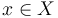, there exists a neighborhood 
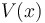so that 
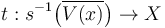is proper.
Note that (Lie) makes sense because (etale) hypothesis implies that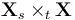 
inherits an M-polyfold structure.
Moreover, (proper) implies that each isotropy group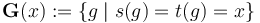 
is finite.
We denote the orbit space by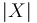 
.
A polyfold structure on a (paracompact, Hausdorff) space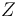 
is simply 
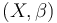where 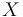is an EP-groupoid and 
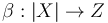is a homeomorphism.
We now illustrate the concept of an EP-groupoid in the following
Example: the EP-groupoid structure of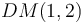 
.
blah blah
