Difference between revisions of "Deligne-Mumford space"

From Polyfolds.org
Jump to: navigation, search
(Created page with "table of contents '''TODO:''' Expand on this copy of a sketch in the moduli space construction For <math>d\geq 2</math>, the moduli space of domains <center><math> \math...")
 
Line 8: Line 8:
 
{\Sigma_{\underline{z}} \sim \Sigma_{\underline{z}'} \;\text{iff}\; \exists \psi:\Sigma_{\underline{z}}\to \Sigma_{\underline{z}'}, \; \psi^*i=i }
 
{\Sigma_{\underline{z}} \sim \Sigma_{\underline{z}'} \;\text{iff}\; \exists \psi:\Sigma_{\underline{z}}\to \Sigma_{\underline{z}'}, \; \psi^*i=i }
 
</math></center>
 
</math></center>
−
can be compactified to form the [[Deligne-Mumford space]] <math>\overline\mathcal{DM}_{d+1}</math>, whose boundary and corner strata can be represented by trees of polygonal domains <math>(\Sigma_v)_{v\in V}</math> with each edge <math>e=(v,w)</math> represented by two punctures <math>z^-_e\in \Sigma_v</math> and <math>z^+_e\in\Sigma_w</math>. The ''thin'' neighbourhoods of these punctures are biholomorphic to half-strips, and then a neighbourhood of a tree of polygonal domains is obtained by gluing the domains together at the pairs of strip-like ends represented by the edges.
+
can be compactified to form the [[Deligne-Mumford space]] <math>\overline\mathcal{M}_{d+1}</math>, whose boundary and corner strata can be represented by trees of polygonal domains <math>(\Sigma_v)_{v\in V}</math> with each edge <math>e=(v,w)</math> represented by two punctures <math>z^-_e\in \Sigma_v</math> and <math>z^+_e\in\Sigma_w</math>. The ''thin'' neighbourhoods of these punctures are biholomorphic to half-strips, and then a neighbourhood of a tree of polygonal domains is obtained by gluing the domains together at the pairs of strip-like ends represented by the edges.

Revision as of 11:11, 24 May 2017

table of contents

TODO: Expand on this copy of a sketch in the moduli space construction

For 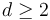d\geq 2, the moduli space of domains

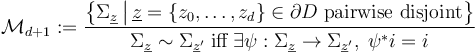
{\mathcal {M}}_{{d+1}}:={\frac {{\bigl \{}\Sigma _{{\underline {z}}}\,{\big |}\,\underline {z}=\{z_{0},\ldots ,z_{d}\}\in \partial D\;{\text{pairwise disjoint}}{\bigr \}}}{\Sigma _{{\underline {z}}}\sim \Sigma _{{\underline {z}'}}\;{\text{iff}}\;\exists \psi :\Sigma _{{\underline {z}}}\to \Sigma _{{\underline {z}'}},\;\psi ^{*}i=i}}

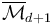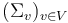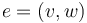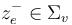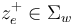can be compactified to form the Deligne-Mumford space \overline {\mathcal {M}}_{{d+1}}, whose boundary and corner strata can be represented by trees of polygonal domains (\Sigma _{v})_{{v\in V}} with each edge e=(v,w) represented by two punctures z_{e}^{-}\in \Sigma _{v} and z_{e}^{+}\in \Sigma _{w}. The thin neighbourhoods of these punctures are biholomorphic to half-strips, and then a neighbourhood of a tree of polygonal domains is obtained by gluing the domains together at the pairs of strip-like ends represented by the edges.

Retrieved from "http://www.polyfolds.org/index.php?title=Deligne-Mumford_space&oldid=281"