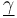Difference between revisions of "Compactified Morse trajectory spaces"
From Polyfolds.org
m |
m |
||
| Line 18: | Line 18: | ||
</center> | </center> | ||
| − | '''TODO:''' smooth evaluation maps <math>{\rm ev}^\pm</math>, length <math>\ell</math> | + | '''TODO:''' smooth evaluation maps <math>{\rm ev}^\pm</math>, length <math>\ell: \overline \mathcal{M}(L,L) \to [0,\infty]</math> given by <math>\ell(\gamma)= a</math> and <math>\ell(\underline{\gamma})=\infty</math> for all generalized (''broken'') Morse trajectories <math>\underline{\gamma}</math> |
Revision as of 11:52, 24 May 2017
Consider a smooth manifold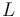 
equipped with a Morse function 
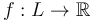and a metric so that the gradient vector field 
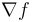satisfies the Morse-Smale conditions. Then the Morse trajectory spaces
![{\begin{alignedat}{4}{\mathcal {M}}(L,L)&=\{\gamma :&[0,a]\;\;\to L&\,|\,{\dot \gamma }=-\nabla f(\gamma ),a\geq 0\},\\{\mathcal {M}}(p^{-},L)&=\{\gamma :&(-\infty ,0]\to L&\,|\,{\dot \gamma }=-\nabla f(\gamma ),\lim _{{s\to -\infty }}\gamma (s)=p^{-}\},\\{\mathcal {M}}(L,p^{+})&=\{\gamma :&[0,\infty )\;\to L&\,|\,{\dot \gamma }=-\nabla f(\gamma ),\lim _{{s\to +\infty }}\gamma (s)=p^{+}\},\\{\mathcal {M}}(p^{-},p^{+})&=\{\gamma :&\mathbb{R} \;\;\;\to L&\,|\,{\dot \gamma }=-\nabla f(\gamma ),\lim _{{s\to \pm \infty }}\gamma (s)=p^{\pm }\}/\mathbb{R} .\end{alignedat}}](/images/math/a/c/3/ac36e80abe76a15538933ab31effdc2f.png)
can - under an additional technical assumption specified in [1] - be compactified to smooth manifolds with boundary and corners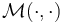 
.
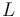These compactifications are constructed such that the codimension-1 strata of the boundary are given by single breaking at a critical point (except in the first case we have to add one copy of to represent trajectories of length 0),
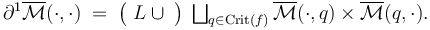
TODO: smooth evaluation maps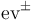 
, length ![\ell :\overline {\mathcal {M}}(L,L)\to [0,\infty ]](/images/math/1/9/9/1999df464cac2fa6d20df6322ce81aea.png)
given by 
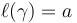and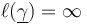 
for all generalized (broken) Morse trajectories 
