Difference between revisions of "Deligne-Mumford space"
From Polyfolds.org
(Created page with "table of contents '''TODO:''' Expand on this copy of a sketch in the moduli space construction For <math>d\geq 2</math>, the moduli space of domains <center><math> \math...") |
|||
| Line 8: | Line 8: | ||
{\Sigma_{\underline{z}} \sim \Sigma_{\underline{z}'} \;\text{iff}\; \exists \psi:\Sigma_{\underline{z}}\to \Sigma_{\underline{z}'}, \; \psi^*i=i } | {\Sigma_{\underline{z}} \sim \Sigma_{\underline{z}'} \;\text{iff}\; \exists \psi:\Sigma_{\underline{z}}\to \Sigma_{\underline{z}'}, \; \psi^*i=i } | ||
</math></center> | </math></center> | ||
| − | can be compactified to form the [[Deligne-Mumford space]] <math>\overline\mathcal{ | + | can be compactified to form the [[Deligne-Mumford space]] <math>\overline\mathcal{M}_{d+1}</math>, whose boundary and corner strata can be represented by trees of polygonal domains <math>(\Sigma_v)_{v\in V}</math> with each edge <math>e=(v,w)</math> represented by two punctures <math>z^-_e\in \Sigma_v</math> and <math>z^+_e\in\Sigma_w</math>. The ''thin'' neighbourhoods of these punctures are biholomorphic to half-strips, and then a neighbourhood of a tree of polygonal domains is obtained by gluing the domains together at the pairs of strip-like ends represented by the edges. |
Revision as of 11:11, 24 May 2017
TODO: Expand on this copy of a sketch in the moduli space construction
For 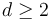 , the moduli space of domains
, the moduli space of domains
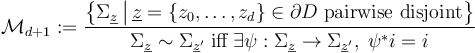
can be compactified to form the Deligne-Mumford space 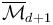 , whose boundary and corner strata can be represented by trees of polygonal domains
, whose boundary and corner strata can be represented by trees of polygonal domains 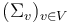 with each edge
with each edge 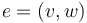 represented by two punctures
represented by two punctures 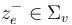 and
and 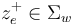 . The thin neighbourhoods of these punctures are biholomorphic to half-strips, and then a neighbourhood of a tree of polygonal domains is obtained by gluing the domains together at the pairs of strip-like ends represented by the edges.
. The thin neighbourhoods of these punctures are biholomorphic to half-strips, and then a neighbourhood of a tree of polygonal domains is obtained by gluing the domains together at the pairs of strip-like ends represented by the edges.